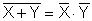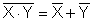Signaalinkäsittelytekniikan laboratorio
Digitaalitekniikan perusteet - luento 3
Merkkikoodeista
Digitaalilaitteissa esitetään erilaisia merkkejä. Merkit voivat olla esimerkiksi kirjaimia,
numeroita, erikoismerkkejä (esim. ¦ « © ß), puoligraafisia merkkejä
tai ohjauskoodeja ( esim.CR, LF, FF, SYN). Merkit esitetään merkkikoodien
avulla:
- jokaista merkkiä vastaa tietty koodi eli bittijono
- merkkikoodin bittien lukumäärä riippuu esitettävien merkkien määrästä: n:llä bitillä voidaan esittää 2n merkkiä
- merkkikoodin bittimäärä on yleensä sama kaikille merkeille
- ASCII-koodi
Aakkosellisten merkkien keskeinen binäärikoodi on ASCII (American Standard Code For
Information Interchange). ASCII koodi käyttää seitsemää bittiä esittämään 128 erilaista
merkkiä (27=128). Merkistö sisältää 94 tulostettavaa kirjainta sekä 32 ohjauskoodia. Tulostettavat
kirjaimet ovat englanninkielisen aakkoston 26 merkkiä sekä isoina että pieninä kirjaimina,
10 numeroa sekä 32 erikoismerkkiä. (Ohjausmerkit eivät tulostu.)
Huomattavaa on siis, että ASCII ei sisällä ns. 'ääkkösiä'. ASCII-koodista on olemassa alueellisia
versioita, joissa jotain erikoismerkkejä on korvattu kansallisilla kirjaimilla.
ASCII-koodi taulukon löydät esim. kirjoista
Logic and Computer Design Fundamentals (Mano & Kime),
The Essence of Digital Design (Wilkinson),
Principles of Digital Design (Gajski)
Fundamentals of Digital Logic with VHDL Design (Brown & Vrasenic)
- ANSI-koodi
ANSI-koodauksessa (American National Standards Institute) käytetään kahdeksaa bittiä, joilla voidaan kuvata yhteensä 256
merkkiä (28=256). Numerot ja kirjaimet ovat vastaavat kuin ASCIIssa, mutta lisäksi koodauksessa on
valmiina kansallisia kirjaimia sekä runsaasti lisää erikoismerkkejä.
- Muita merkkikoodeja (Yllämainitut ovat ylivoimaisesti tärkeimmät.)
DOS-merkistöt
- kuusi vähän toisistaan poikkeavaa merkistöä, yksi näistä pohjoismainen (sis. ääkköset)
- 8 bittiä, 256 merkkiä
- numerot, kirjaimet ja erikoismerkit kuten ASCIIssa
- lisäksi kansallisia kirjaimia, lisää erikoismerkkejä, puoligraafisia merkkejä sekä
matemaattisia symboleja
- käytössä DOS -ympäristössä
Baudot -koodi
- käytössä esim. joissakin Telex -laitteissa
- 5 bittiä, 32 merkkiä
- merkistön laajennus tasonvaihtomerkeillä
Virheen havaitseminen ja korjaus
Kun tietoa muutetaan muodosta toiseen, talletetaan tai erityisesti, kun sitä siirretään,
syntyy virheitä. Voidaan asettaa erilaisia rajoja sille, missä määrin esiintyessään virheet
ovat häiritseviä. Virheiden häiritsevyys vaihtelee siirrettävän datan, sen pakkauksen ja
tarkoituksen mukaan. (Esim. tavallisessa äänen siirrossa voi esiintyä paljonkin virheitä,
ennen kuin käyttäjä havaitsee ne häiritsevänä naksahteluna. Toisaalta taas
jpeg -kuvaformaatissa yksikin virheellinen merkkikoodi voi pilata koko kuvan.)
Tiedonsiirrossa on tärkeää huomata virheet vastaanottopäässä. Kun virhe huomataan, voidaan
pyytää virheellisen kohdan uudelleenlähettämistä. On myös olemassa virhettä korjaavia
koodaustapoja. Virheen havaitseminen perustuu redundanssin lisäämiseen.
Tämä tarkoittaa sitä, että vain osa biteistä käytetään varsinaisen datan siirtoon. Loppuosa biteistä
on joko toistoa (esim. sama bitti lähetetään kahteen kertaan) tai se tulkitaan
virhekoodiksi. Jos sanaan tulee virhe matkalla, tulkitaan se osaksi virhekoodia ja joko
pyydetään lähettämään uudelleen tai jätetään huomioimatta sanomaa tulkittaessa.
Erilaisia virheentarkistus tai korjausmenetelmiä:
Pariteettitarkastus:
Pariteettibitin käyttö
Pariteettibitin käyttö perustuu siihen, että pakotetaan jokainen koodaussana (joka on siis tietyn mittainen bittijono) pariteetiltaan
samanlaiseksi:
- Jos koodaussanassa on parillinen määrä ykkösiä, on käytetty pariteetti parillinen (even).
- Jos koodaussanassa on pariton määrä ykkösiä, on käytössä luonnollisesti pariton pariteetti (odd).
Pariteetin muodostus perustuu siihen, että jokaiseen sanaan lisätään ylimääräinen bitti
(pariteettibitti), jonka arvo laitetaan lähetyspäässä joko ykköseksi tai nollaksi siten,
että saadaan kaikkiin sanoihin sama pariteetti (siis pariton tai parillinen pariteetti).
Vastaanottopäässä tarkastetaan, kunkin
sanan pariteetti ja jos löydetään pariteetiltaan muista poikkeava sana, voidaan päätellä
virheen tapahtuneen.
Pariteettitarkastuksessa virhe huomataan vastaanottavassa päässä, mutta sitä ei voida korjata
paitsi pyytämällä virheellisen kohdan uudelleenlähetystä. Toinen menetelmän heikkous on, että
se ei huomaa parillista määrää virheitä samassa sanassa. (Jos siis kaksi bittiä kääntyy nurin
päin, säilyy pariteetti.) Tarkastus sopii kätevästi esim. ASCII -merkistöön. Tällöin pidennetään jokainen
7-bittinen sana, lisäämällä niihin pariteettibitti. (Mikä nostaa sanapituuden 8-bittiin eli
yhteen tavuun. 8-bittiä on sikäli hyvä sanapituus, että tietokoneen sanat ovat 8-bittisiä
tai 8-bitin monikertoja.)
Esimerkki pariteettitarkastuksesta löytyy alla olevan esimerkin lisäksi toisen kierroksen harjoituksista.
Esimerkki 1
Lähetetään sana 'Digis' ASCII-koodattuna. (ASCII-koodi saadaan esim. Internetistä tai kirjallisuudesta, kuten edellä oli todettu)
Sana ASCII-koodattuna on : 100 0100 110 1001 110 0111 110 1001 111 0011
Käytetään paritonta pariteettia eli otetaan 7 bitin ryhmiä ja lisätään joko 0 tai 1 ryhmän eteen, jotta saadaan pariton määrä ykkösiä 8 bitin sarjaan.
Saadaan: 1100 0100 1110 1001 0110 0111 1110 1001 0111 0011
(ykkösiä) |--3 kpl--| |-5 kpl--| |--5 kpl--| |-5 kpl--| |-5 kpl---| eli jokaisen kirjaimen kohdalla pariton määrä.
Vastaanottopäässä tiedetään, että on käytetty paritonta pariteettia. Tarkastetaan siis jokaisen vastaanotetun kirjaimen kohdalla pariteetti.
Vastaanotettu bittijono on: 1100 0100 1111 1001 0110 0111 1110 1001 1111 0111
(ykkösiä tässä bittijonossa) |-3 kpl --| |-6 kpl--| |--5 kpl--| |-5 kpl--| |--7 kpl--|
Kirjaimessa numero 2 on siis tullut virhe, koska ykkösten määrä on parillinen vaikka sen piti olla pariton. Tästä kirjaimesta pyydetään uudelleenlähetys ja tulkitaan vastaanotettu ASCII-koodi
Vastaanotettu ASCII-koodi on: 100 0100 110 1001 110 0111 110 1001 111 0111
ja tämä tulkittuna on: 'Digiw' !! Missä meni vikaan ??
Pariteettibitti on siis yksinkertainen tapa tarkastaa data, mutta siinä on omat puutteensa
Hamming -koodaus
Hamming -koodauksessa käytetään montaa pariteettibittiä yhtäaikaa, jolloin virheellinen
bitti voidaan myös paikallistaa ja korjata. (Eli kyseessä on virheenkorjaava koodaus.)
Koodauksesta havaitaan kaikki yhden bitin virheet, muut virheet eivät tule ilmi.
- n:lle databitille tarvitaan k pariteettibittiä siten, että n + k + 1 = < 2k
- bittipaikat numeroidaan 1 ... n + k
- pariteettibitit sijoitetaan kakkosen potenssin mukaisille bittipaikoille: 1, 2, 4, 8, jne
- Esim: b1, b2,b3,
b4, b5, b6, b7,
b8, ..
- Kukin pariteettibitti muodostetaan osalle databiteistä käyttäen parillista pariteettia.
- b1 muodostetaan databiteille, joiden paikkanumeron
binääriesityksen vähiten merkitsevä bitti on 1 (b3,b5,
b7, b9..)
- b2 muodostetaan biteille, joiden paikkanumeron binääriesityksen
toiseksi vähiten merkitsevä bitti on 1 (b3,b6,b7,b10..)
- Koodia tulkittaessa muodostetaan pariteettibittejä vastaavat tarkastusbitit C1, C2,
C4.. kustakin pariteettibitistä ja sen muodostamiseen käytetyistä databiteistä.
- Tarkistusbitti muodostetaan kuin se olisi pariteettibitti.
- Jos kaikki tarkistusbitit ovat nollia, koodi on virheetön. Jos eivät, voidaan tarkistusbittien
arvoista päätellä virheen paikka.
Monimutkaista siis. Kannatti lukea yleissivistyksen vuoksi.. Jos aihe kiinnostaa enemmän, löytyy esimerkiksi
Internetistä paljonkin asiaa Hamming koodauksesta. Todella innokkaille mainittakoon, että käytännön
harjoituksena Hamming-kooderin ohjelmointi esimerkiksi
C-kieltä käyttäen ei ole mikään mahdoton urakka.
Esimerkki 1
Lähetetään saman bittijonon alku kuin pariteettiesimerkissämme eli sanan 'Digis' ensimmäinen kirjain 'D' ASCII-muodossa. Lähetetään se kahteen eri vastaanottopaikkaan, joista toiseen on hyvä ja toiseen huono yhteys.
Saadaan: 100 0100
Nyt meillä on 7 databitin ryhmä. Tarvitaan siis k pariteettibittiä siten, että n + k + 1 = < 2
k
Mikäli k = 3. Tällöin n + k + 1 = 7 + 3 + 1 = 11 ja 2
k = 2
3 = 8. Todetaan, että 11 < 8 mikä ei pidä paikkaansa!
Mikäli k = 4. Tällöin n + k + 1 = 7 + 4 + 1 = 12 ja 2
k = 2
4 = 16. Todetaan, että 12 < 16 mikä on totta.
Numeroidaan bittipaikat 1 --> 11, jolloin saadaan : b
1, b
2, b
3, b
4, b
5, b
6, b
7, b
8, b
9, b
10, b
11.
Sijoitetaan pariteettibitit kakkosen potenssin mukaisille paikoille eli 1,2,4, ja 8
Tällöin saadaan seuraava bittijono: b
1,b
21,b
4,
000,b
8100 (Tummennetut bitit ovat alkuperäiset ASCII-koodista saadut bitit järjestyksessä)
Parillista pariteettia käyttäen
b
1 muodostetaan databiteille (b
3,b
5,b
7,b
9,b
11). Kyseiset bitit ovat 10010.
Parillista pariteettia käyttäen saadaan b
1=0
Vastaavasti
b
2 muodostetaan databiteille (b
3,b
6,b
7,b
10,b
11). Kyseiset bitit ovat 10000.
Parillista pariteettia käyttäen saadaan b
1=1
Edelleen
b
4 muodostetaan databiteille (b
5,b
6,b
7). Kyseiset bitit ovat 000.
Parillista pariteettia käyttäen saadaan b
1=0
Lopuksi
b
8 muodostetaan databiteille (b
9,b
10,b
11). Kyseiset bitit ovat 100.
Parillista pariteettia käyttäen saadaan b
1=1
Lopullinen Hamming-koodattu bittijono on siis: 01100001100
Vastaanotto 1: Vastaanotetaan bittijono 01100001100
Tarkastetaan pariteettibitit:
b
1 muodostetaan databiteille (b
3,b
5,b
7,b
9,b
11). Kyseiset bitit ovat 10010.
Parillista pariteettia käyttäen saadaan b
1=0
b
2 muodostetaan databiteille (b
3,b
6,b
7,b
10,b
11). Kyseiset bitit ovat 10000.
Parillista pariteettia käyttäen saadaan b
1=1
jne. jne.
Lopuksi saadaan seuraavat pariteettibitit:
- b1 = 0
- b2 = 1
- b4 = 0
- b8 = 1
Nämä vastaavat täysin niitä pariteettibittejä jotka oli muodostettukin lähetyspäässä. Siis vastaanotto on onnistunut.
Vastaanotto 2: Vastaanotetaan bittijono 01100101100
Tarkastetaan pariteettibitit:
b
1 muodostetaan databiteille (b
3,b
5,b
7,b
9,b
11). Kyseiset bitit ovat 10010.
Parillista pariteettia käyttäen saadaan b
1=0
b
2 muodostetaan databiteille (b
3,b
6,b
7,b
10,b
11). Kyseiset bitit ovat 11000.
Parillista pariteettia käyttäen saadaan b
1=0
b
4 muodostetaan databiteille (b
5,b
6,b
7). Kyseiset bitit ovat 010.
Parillista pariteettia käyttäen saadaan b
1=1
b
8 muodostetaan databiteille (b
9,b
10,b
11). Kyseiset bitit ovat 100.
Parillista pariteettia käyttäen saadaan b
1=1
Lopuksi saadaan seuraavat pariteettibitit:
- b1 = 0
- b2 = 0
- b4 = 1
- b8 = 1
Huomataan, että b
2 ja b
4 ovat väärin!. Seuraavaksi tarkastellaan mikä bitti on kääntynyt:
- b2 huomioi databitit (b3,b6,b7,b10,b11). Joku näistä on mennyt väärin.
- b4 huomioi databitit (b5,b6,b7). Joku näistä on mennyt väärin. Kun huomioidaan myös b2:n bitit voidaan sanoa, että jompikumpi biteistä (b6,b7) on väärin.
- b1 huomioi databitit (b3,b5,b7,b9,b11). Tämä pariteettibitti oli oikein, joten myös bitti b7 on oikein.
- Voidaan lopuksi päätellä siis, että bitti b6 on kääntynyt ympäri ja tämä voidaan nyt korjata kun tiedetään missä kohtaa virhe sijaitsee!!
Kytkentäalgebra ja logiikkapiiri
Digitaalilaitteet suorittavat erittäin monimutkaisia usein laskennallisia tehtäviä. Pohjimmaiset
operaatiot ovat kuitenkin hyvin yksinkertaisia. Digitaalipiirien suunnittelu perustuu ns.
Boolean algebraan, joka muistuttaa matemaattista
logiikkaa, joskaan ei vastaa sitä kaikilta ominaisuuksiltaan.
Digitaalilaitteet toteutetaan kytkentäalgebralla. Kytkentäalgebra pyrkii toimimaan Boolean
algebran mukaan. (Nopeissa ja monimutkaisissa sovelluksissa esim. porttien hitaus aiheuttaa
rajoituksia.) Kytkentäfunktiot eli loogiset funktiot muodostetaan logiikkapiireillä, joita on
hyvin eri tyyppisiä. Esimerkiksi porttipiirit, joiden käsittely aloitetaan tällä luennolla ovat
loogisia piirejä.
Digitaalisella signaalilla on kaksi arvoa (0 ja 1). Signaaleista muodostetaan uusia signaaleja tietyin
perustein. (Käytännössä tämä tarkoittaa sitä, että yhtä tai useampaa signaalia kuljetetaan
erilaisten piirielementtien läpi, jolloin muodostuu erilainen uusi signaali. Ehkäpä esimerkki
selvittää.)
Esimerkki signaaleista
Esimerkkimme on elävästä elämästä tilanne kun ylitetään ajorataa liikennevalojen kohdalta.
Meillä on kaksi ottosignaalia (nämä siis tulevat laitteeseen sisään), joiden perusteella teemme tienylitys päätöksen:
- EI_AUTO (autoa ei näy): signaalin arvo on 1, kun autoja ei näy; signaalin arvo on 0, kun autoja on tulossa
- V_VALO (vihreä valo palaa): signaalin arvo on 1, kun valo palaa; signaalin arvo on 0, kun valo ei pala
Sovitaan, että on turvallista ylittää tie, mikäli autoja ei näy ja vihreä valo palaa.
Halutaan antosignaali (signaali, jonka laite antaa ulos), joka kertoo milloin on turvallista ylittää tie. Annetaan
antosignaalille nimeksi TURVA. Tällöin voidaan muodostaa TURVA signaalille looginen ehto: TURVA = EI_AUTO ja V_VALO. (Mikä siis
tulkitaan, että TURVA signaali saa arvon 1, jos sekä EI_AUTO = 1 että V_VALO = 1)
Tässä esimerkissä kaikki signaalit ovat muuttujasignaaleita. Niiden arvo siis voi vaihdella
ajanhetkestä toiseen. (Vakiosignaali olisi aina joko 0 tai 1.)
Loogiset perusfunktiot
Loogiset perusfunktiot muodostavat digitaalilogiikan perustan. Näistä funktioista voidaan muodostaa
kaikki muut loogiset funktiot. Loogisia muuttujia merkitään isoilla kirjaimilla (esim. A, B, C, D, …). Loogiset
perusfunktiot ovat EI, TAI ja JA. (NOT, OR, AND).
EI (NOT) -funktio
EI on negaatiofunktio. Jos sisääntulevan muuttujan (ottosignaalin) arvo on 1, tulee sen lähtöarvoksi 0. Jos
muuttujan arvo on 0, saa funktio arvon 1. (EI-funktio kääntää siis bitin nurinpäin.)
EI -funktio merkitään lausekkeissa pilkulla A' tai viivalla muuttujan päällä:
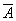
Totuustaulu on yksiselitteinen tapa esittää funktio. Totuustaulussa esitetään
funktion sisäänottamat signaalit ja ulostulevat signaalit siten, että kaikki mahdolliset
tapaukset käsitellään. EI-funktion totuustaulu näyttää tältä:
Eli F = A' tai toisella tapaa merkittynä F = 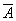
TAI (OR) -funktio
EI -funktio oli yhden muuttujan funktio. TAI funktio voi käsitellä kahta tai useampaa ottosignaalia
yhtä aikaa. (Puhutaan 2-otto TAI -porteista, 3-otto TAI -porteista jne..) TAI -funktio saa arvon yksi
aina, kun yksikin ottosignaaleista on arvoltaan 1. Jos kaikki ottosignaalit ovat nollia, saa
TAI -funktiokin arvon nolla.
Kahden muuttujan TAI-funktio merkitään seuraavasti: F = A + B. Tässä on huomattava, että TAI -
funktio ei noudata matematiikan vaan Boolean logiikan laskusääntöjä, mikä nähdään totuustaulusta:
Input
A | Input
B | Output
F |
|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
(Siis + ei tarkoita tässä yhteenlaskua, vaan operaatiota TAI. Tämä selittää, miksi voidaan väittää,
että A + B = 1.)
JA (AND) -funktio
JA -funktio muistuttaa kertolaskua. Myös se voi käsitellä kahta tai useampaa ottosignaalia
yhtä aikaa. JA -funktio saa arvon nolla, jos yksikin sen ottosignaaleista on nolla. Vain, jos
kaikkien ottosignaalien arvo on yksi, saa myös funktio arvon yksi. Lausekkeissa JA -funktio
merkitään kertolaskunotaatiolla: 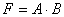 . Usein kertomerkki jätetään
välistä ja kirjoitetaan yksinkertaisesti F = AB. Tätä käytetään erityisesti lausekkeissa, joissa on
sekä JA että TAI operaatiota. (Jolloin voidaan ilmaista esim: F = AB + AC + BDE.)
. Usein kertomerkki jätetään
välistä ja kirjoitetaan yksinkertaisesti F = AB. Tätä käytetään erityisesti lausekkeissa, joissa on
sekä JA että TAI operaatiota. (Jolloin voidaan ilmaista esim: F = AB + AC + BDE.)
JA -funktion totuustaulu näyttää siis seuraavalta:
Input
A | Input
B | Output
F |
|---|
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
Kytkentäalgebran teoreemoja
eli Boolean Algebra
Loogiset funktiot toimivat osittain suoraan binääriaritmetiikan mukaan. Erojakin löytyy,
yleisin lienee TAI -funktiossa oleva 1 + 1 = 1. Kytkentäalgebrassa JA -funktiota sanotaan
loogiseksi tuloksi ja TAI -funktiota loogiseksi summaksi.
Kytkentäalgebran (eli ns. Boolean algebran) tärkeimpiä teoreemoja on listattu alle:
|
Yhden muuttujan teoreemoja: |
|---|
| X + 0 = X | | X × 1 = X | |
| X + 1 = 1 | | X × 0 = 0 | |
| X + X = X | | X × X = X | |
| X + X' = 1 | | X × X' = 0 | |
|
Monen muuttujan teoreemoja: |
|---|
| X + Y = Y + X | | XY = YX | kommutatiivisuus |
| X + (Y + Z) = (X + Y) +Z | | X(YZ) = (XY)Z | assosiatiivisuus |
| X( Y + Z) = XY + XZ | | X + YZ = (X + Y)(X + Z) | distributiivisuus |
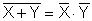 | |
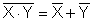 | De Morgan |
Nämä siis ovat suoraan laskusääntöjä, joita saa (ja pitää) käyttää digitaalisuunnittelussa. Näiden sääntöjen mukaan
toimivat myös digitaalisuunnittelussa käytettävät portit, jotka esitellään myöhemmin. Monen muuttujan teoreemien
viimeisellä rivillä esitetään
ns. De Morganin kaavat. Ne käsittelevät siis komplementtia sellaisessa tapauksessa, jossa
komplementoidaan kerralla enemmän kuin yksi muuttuja (yleensä lauseke tai osa siitä).
De Morganin teoreema on tärkeä suunnittelussa, koska sen avulla voidaan saada erilaisia
toteutuksia samalle loogiselle lausekkeelle. De Morganin teoreema voidaan yleistää n >=2
muuttujalle. (Jätetään lukijan pohdittavaksi, miten.)
Teoreemoista puhutaan paljon lisää myöhemmin, kun käsitellään kytkentäfunktioita. (Kytkentäfunktio
on siis lauseke, joka sisältää edellä esitettyjä funktioita ja joka voidaan toteuttaa lopulta
esim. porttipiireillä.)
Porttipiirit
Loogiset funktiot ja lausekkeet toteutetaan yleensä sähköisillä piireillä. Tällä
kurssilla tarkastellaan porttipiiritoteutuksia. Sähköisissä piireissä tietty jännitetaso
vastaa tiettyä loogista tilaa.
Esimerkkinä CMOS-logiikkapiirin vastaavuudet:
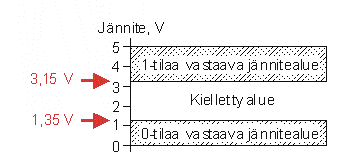
Siis kaikki eri jännitteet 3,15 voltin ja 5 voltin välillä tulkitaan loogiseksi ykköseksi, kaikki alle 1,35 voltin jännitteet tulkitaan loogiseksi nollaksi.
Jännitteellä on tietty sallittu vaihteluväli, koska olisi hankalaa ja kallista vaatia tasan tiettyä jännitettä.
Virheiden eliminoimiseksi välillä on myös kielletty alue, joka pyrkii estämään vahingossa tilasta toiseen
lipsuvan jännitteen.
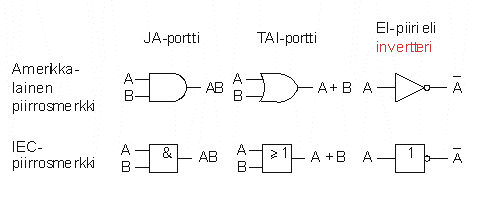
Perusfunktioita (JA, TAI, EI) vastaavat omat porttipiirinsä, joiden piirrosmerkit on
taulukoitu alle. Kurssilla pyritään käyttämään IEC standardin mukaisia merkkejä, mutta käytännön elämässä
näkee paljon myös amerikkalaisen standardin mukaisia merkkejä.
Kun piirretään yksittäisiä portteja tai piirikaavioita laitetaan se, mitä portti ottaa sisäänsä (ottosignaali/-signaalit)
vasemmalle puolelle ja antosignaali oikealle puolelle. Jos piirretään aikakaavioita, kulkee aika vasemmalta oikealle.
Kytkentäfunktion kolme esitystapaa
Looginen funktio, totuustaulu ja piirikaavio ovat elementtejä, jotka kaikki vastaavat toisiaan
ja tarvittaessa yhdestä esitystavasta voidaan johtaa muut kaksi. Looginen funktio lienee tässä vaiheessa tutuin.
Looginen funktio voi olla esimerkiksi F = X + Y'Z tai G = (D + E)(MKAY + PVALO) + B'. Looginen
funktio voidaan kytkentäalgebran säännöstön mukaan muuntaa muodosta toiseen. Usein lausekkeen
muokkaaminen ja yksinkertaistaminen kannattaa, koska näin saadaan aikaan yksinkertaisempi
piiritoteutus.
Totuustaulu taas käy taulukkomuodossa läpi kaikki mahdolliset kombinaatiot muuttujista (input) ja
osoittaa, mikä on funktion arvo (output) kullakin muuttujien kombinaatiolla. Alla on esimerkkinä loogisen funktion
F = X + Y'Z totuustaulu:
Input
X | Input
Y |
Input
Z | Output
F |
|---|
| 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 1 |
| 0 | 1 | 0 | 0 |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 0 | 1 |
| 1 | 0 | 1 | 1 |
| 1 | 1 | 0 | 1 |
| 1 | 1 | 1 | 1 |
Ylläoleva totuustaulu on muodostettu loogisesta funktiosta seuraavasti:
Merkitään ensin sarakkeisiin X, Y ja Z kaikki mahdolliset kombinaatiot, joita on siis 8 erilaista (000 -> 111)
Tämän jälkeen merkitään F sarakkeeseen ykkönen kaikille riveille joissa toteutuu Y=0 ja Z=1. Tämä vastaa loogisen funktion lausekkeesta osaa Y'Z
Lopuksi merkitään vielä ykköset F sarakkeeseen kaikille riveille joissa toteutuu X=1. Näin on muodostettu loogista funktiota X+Y'Z vastaava totuustaulu.
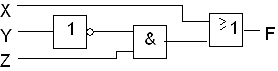
Piirikaavio on taas havainnollinen kuvaus funktion toteuttavasta piiristä. Piirikaaviota piirrettäessä
muistetaan, että ottosignaalit tulevat yleensä vasemmalta ja anto laitetaan oikealle. (Monimutkaisissa
piireissä tämä sääntö tosin voidaan unohtaa.) Piirikaavio voidaan piirtää suoraan funktion lausekkeesta.
Esimerkkinä on piirretty lausekkeen F = X + Y'Z piirikaavio. (Ensin siis suoritetaan komplementaatio Y:lle käyttäen EI-porttia,
sitten Y':n ja Z:n JA-operaatio (Y'Z) ja lopuksi TAI-operaatio JA:n tuloksen ja X:n välillä (X + Y'Z.))
Paluu päävalikkoon
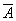
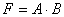 . Usein kertomerkki jätetään
välistä ja kirjoitetaan yksinkertaisesti F = AB. Tätä käytetään erityisesti lausekkeissa, joissa on
sekä JA että TAI operaatiota. (Jolloin voidaan ilmaista esim: F = AB + AC + BDE.)
. Usein kertomerkki jätetään
välistä ja kirjoitetaan yksinkertaisesti F = AB. Tätä käytetään erityisesti lausekkeissa, joissa on
sekä JA että TAI operaatiota. (Jolloin voidaan ilmaista esim: F = AB + AC + BDE.)